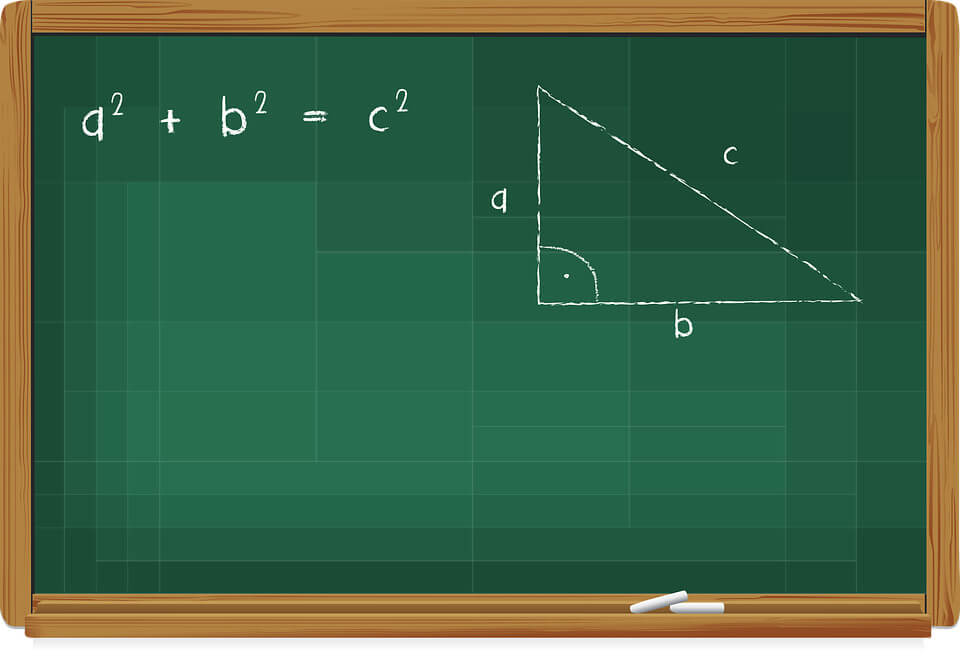
Uno dei teoremi più famosi di tutta la Geometria Euclidea è il Teorema di Pitagora. Esso afferma che il quadrato costruito sull’ipotenusa di un triangolo rettangolo è equivalente alla somma dei quadrati costruiti sui cateti del triangolo considerato. La sua dimostrazione viene attribuita, come dice il nome, al matematico greco Pitagora, anche se è probabile che altre civiltà abbiano scoperto questo teorema ben prima della sua nascita (o comunque, indipendentemente da Pitagora).
Enunciato:
In un triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla somma delle aree dei quadrati costruiti sui cateti.
Dimostrazione:
- disegniamo un triangolo rettangolo ABC con l'angolo retto in A
- indichiamo con h il cateto con C1 l'ipotenusa e con b l' altro cateto

-costruiamo su ciascun lato del triangolo un quadrato avente per base quel lato
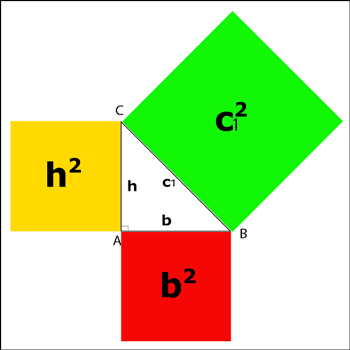
l'interpretazione geometrica del Teorema di Pitagora è semplice: l'area del quadrato C1 costruito sull'ipotenusa c1; è uguale alla somma delle aree dei quadrati h, b costruiti sui due cateti h e b. In riferimento alla figura, la somma della porzione gialla e rossa è uguale all'area della porzione verde. In formule:
AreaC1=Area h + Area b
ricordando che l'area del quadrato si ottiene elevando al quadrato la misura del lato, abbiamo:
Area h = area del quadrato h = h²( cateto al quadrato)
Area b = area del quadrato b = b²(cateto al quadrato)
Area C1= area del quadrato C1= c1² (ipotenusa al quadrato)
Possiamo allora riassumere il teorema di Pitagora alla seguente formula:
c1²= h²+b²
Da questa relazione è possibile ricavere velocemente le formule inverse necessarie :
h²=c1²-b²
b²=c1²-h²
Per il calcolo dei lati direttamnente dall'enunciato del teorema di Pitagora basta considerare le precedenti uguaglianze ed estrarre la radice quadrata; Otteniamo così:
c1=√(h²+b²)
h=√(c1²-b²)
b=√(c1²-h²)